Fibonacci Word

Coding in processing

You are probably familiar with the Fibonacci sequence where each subsequent number is a sum of previous two numbers.

A simple mathematical representation of Fibonacci sequence would be written as: F(n)=F(n-1)+F(n-2) for n>1.

This would result in a sequence:
0,1,1,2,3,5,8,13,21,34,55,89,…

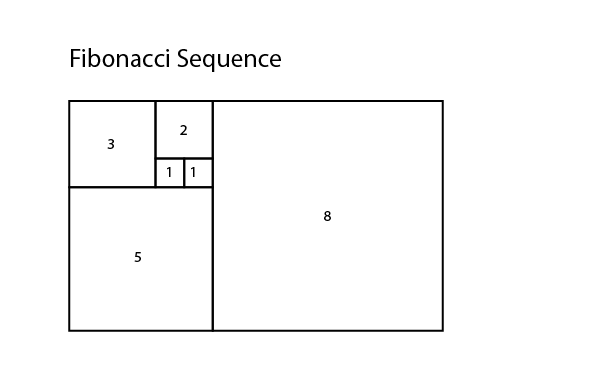
Fibonacci sequence is also closely related to the Golden Ratio. Here is a simple representation of squares whose sides are Fibonacci numbers:

Fibonacci Word

Fibonacci Word is a special sequence of binary digits, but also has some great fractal qualities. When I learned about it, I was really interested to visualize it myself and experience the magic of this sequence.

Fibonacci word is formed by repeating and concatenating the binary digits in the same way as in Fibonacci sequence. You can take any two digits or characters to create this sequence. For the sake of this article, we will go with “0” and “1”. As you can see below, we will start the sequence with the first two digits and then move on to form the third, fourth, etc.

The logic for the sequence is:
Let S(0) be “0” and S(1) be “01”. Now S(n)=S(n-1)S(n-2)